مدار معادل ترانسفورماتور

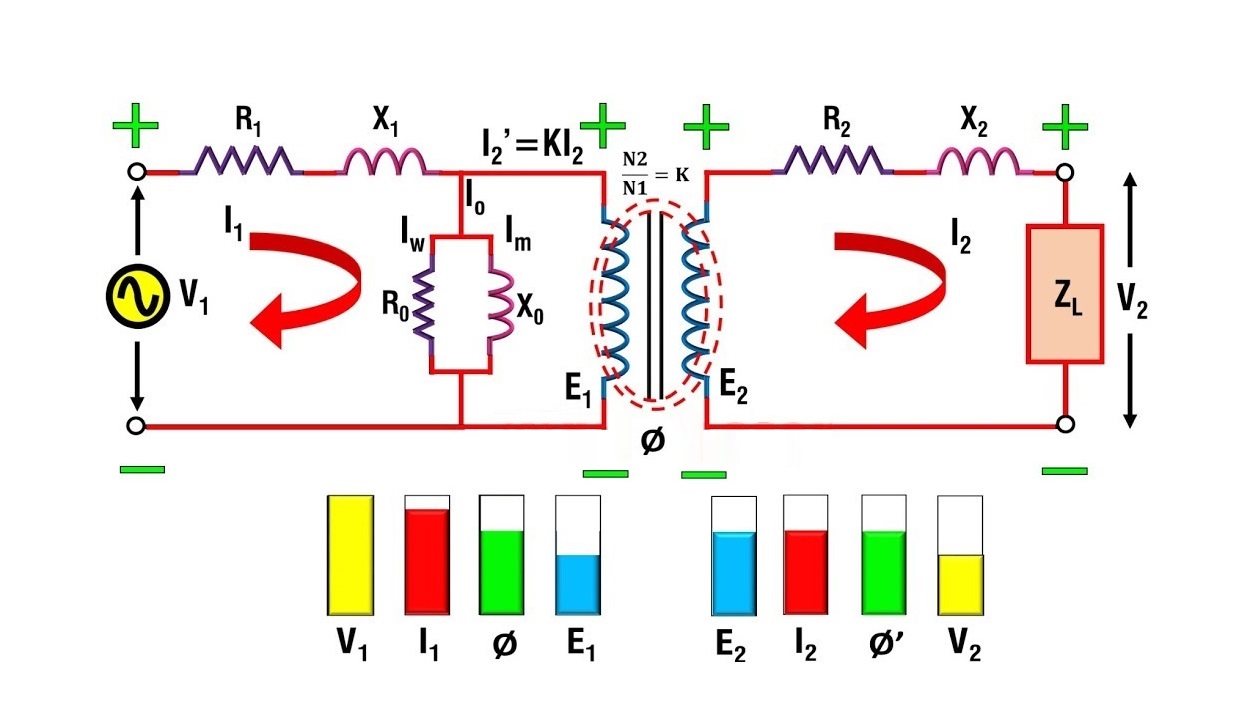
همه ترانسفورماتورها، ویژگی‌ها و پارامترهایی از قبیل مقاومت سیم‌پیچ، هسته با نفوذپذیری محدود، شار نشتی و تلفات هیسترزیس و جریان فوکو دارند. این موارد را می‌توان در قالب مدار معادل ترانسفورماتور بیان کرد که تحلیل آن را ساده می‌کند.در این آموزش، ترانسفورماتور غیرایده‌آل یا عملی را بررسی کرده و مدار معادل آن را به دست می‌آوریم.

مشخصه‌های ترانسفورماتور غیرایده‌آل

شکل 1، ترانسفورماتور غیرایده‌آلی را نشان می‌دهد که می‌توان مشخصات زیر را برای آن نام برد:

1. ترانسفورماتور، نشتی شار دارد و بدین معنی است که همه شار تولیدی یک سیم‌پیچ، از سیم‌پیچ دیگر نمی‌گذرد.
2. سیم‌پیچ‌های اولیه و ثانویه مقاومت دارند و اگر ولتاژ (منبع ولتاژ) v1 اعمال شود، ولتاژ القایی با آن برابر نیست (v1≠e1). به صورت مشابه، v2≠e2.
3. هسته مغناطیسی، کاملاً نفوذپذیر نیست و برای مغناطیس شوندگی به یک mmf محدود نیاز دارد.
4. از آن‌جایی که شار هسته متناوب است، تلفات هیسترزیس و جریان فوکو وجود خواهد داشت که مجموع آن‌ها تلفات هسته یا آهن نامیده می‌شود.

مدار معادل ترانسفورماتور

در تشکیل مدار معادل ترانسفورماتور دو سیم‌پیچه شکل 1، باید مشخصات یک ترانسفورماتور واقعی را مدل کنیم.

مدار اولیه ترانس را در نظر بگیرید. معادله ولتاژ حلقه به صورت زیر است:

که در آن، R1 مقاومت سیم‌پیچ اولیه و N1 تعداد دورهای آن است.

شار Φ1 سیم‌پیچ اولیه برابر با مجموع شار متقابل Φm و شار نشتی Φ11‌ است.

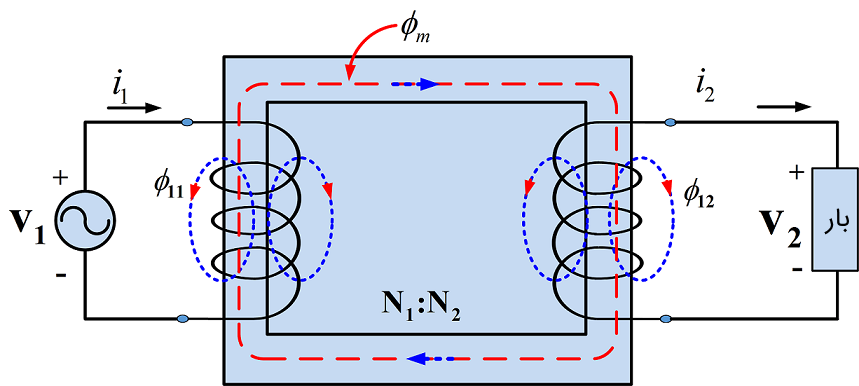
شکل 1: یک ترانسفورماتور واقعی

بنابراین، می‌توان معادله (۱) را به صورت زیر نوشت:

از آن‌جایی که شار نشتی، تابعی خطی از جریان اولیه i1 است، جمله دوم سمت راست معادله (۳) را می‌توان برحسب اندوکتانس سیم‌پیچ اولیه نوشت. بنابراین،

معادله ولتاژ ثانویه نیز به شرح زیر است:

با توجه به جهت شار، شار ثانویه را می‌توان به عنوان اختلاف بین شار متقابل و شار نشتی ثانویه بیان کرد:

با جایگذاری معادله (6) در معادله (5)، داریم:

مشابه سیم‌پیچ اولیه، شار نشتی تابعی خطی از جریان ثانویه i2 است. بنابراین، معادله (۷) را می‌توان با استفاده از اندوکتانس سیم‌پیچ ثانویه بازنویسی کرد:

جملات آخر معادلات (4) و (8)، ولتاژ القایی سیم‌پیچ‌های اولیه و ثانویه را نشان می‌دهند:

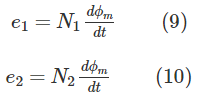
با تقسیم رابطه (9) بر رابطه (10)، نسبت ولتاژ به دست می‌آید:

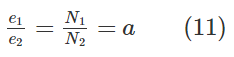
شکل 2، مدار معادل ترانسفورماتور را نشان می‌دهد. اجزای مدار برای مدل‌سازی مغناطیس‌‌شوندگی و تلفات هسته به کار می‌روند که به سمت اولیه و ثانویه افزوده خواهند شد. در شکل 2، سلف Lm1، مغناطیس‌شوندگی هسته و Rc1 تلفات هسته (تلفات هیسترزیس و جریان فوکو) را نشان می‌دهد که به صورت موازی در سمت اولیه ترانسفورماتور متصل می‌شوند. اجزای مربوط به هسته (Rc1 و Lm1)، معمولاً در ولتاژ نامی ارجاع داده شده به سمت اولیه محاسبه می‌شوند. اساساً فرض می‌کنیم این عناصر در شرایط نامی یا نزدیک به آن، ثابت می‌مانند.

مدار معادل فازوری ترانسفورماتور

مدار معادل فازوری ترانسفوراتور، در شکل ۳ نشان داده شده است. راکتانس‌ها را می‌توان با ضرب اندوکتانس‌ها در فرکانس زاویه‌ای ω=2πf به دست آورد که f فرکانس است. نسبت دور a=N1/N2 تقریباً برابر نسبت ولتاژ V1/V2 است که V1 و V2 ولتاژ نامی اولیه و ثانویه هستند و سازنده آن‌ها را ارائه می‌کند.

شکل 2: مدار معادل ترانسفورماتور

 

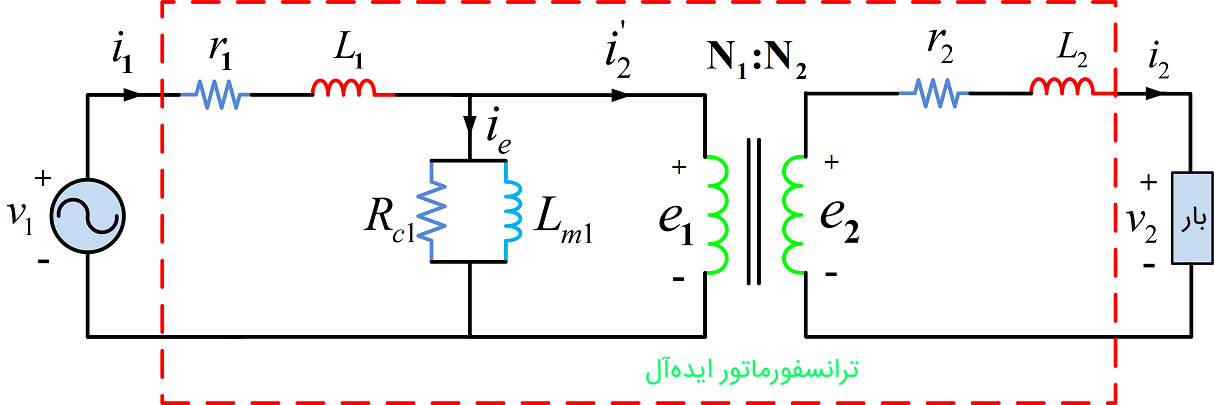
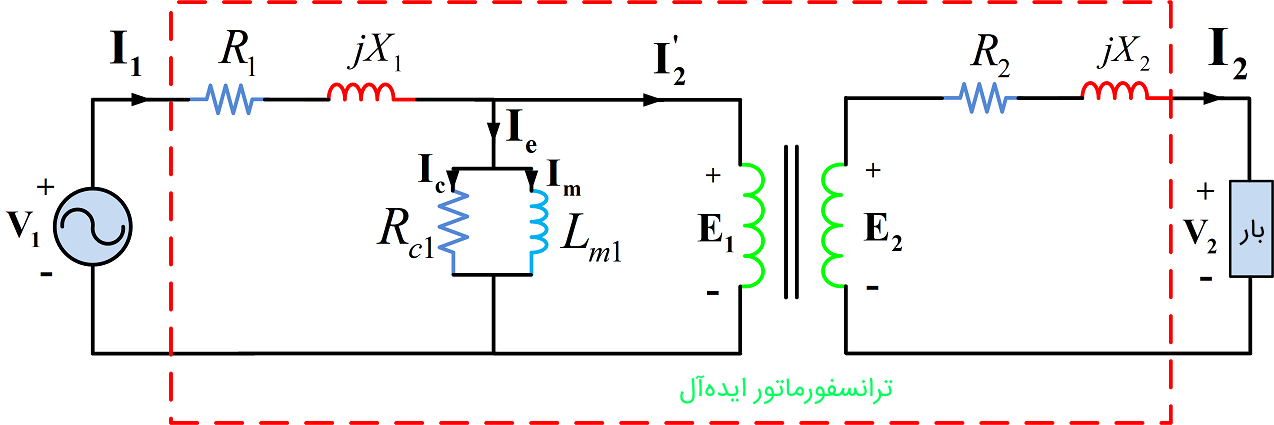
شکل 3: مدار معادل فازوری ترانسفورماتور

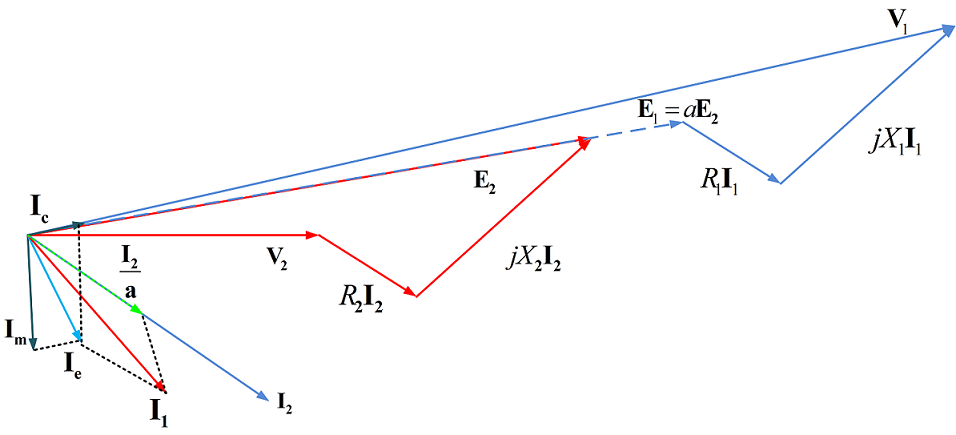
نمودار فازوری برای یک بار سلفی پس‌فاز متصل به ثانویه ترانس شکل ۳، در شکل ۴ نشان داده شده است.

نمادهای مدار، بیان‌گر پارامترهای زیر هستند:

• E1 = ولتاژ القایی اولیه
• E2 = ولتاژ القایی ثانویه
• V1 = ولتاژ ترمینال اولیه
• V2 = ولتاژ ترمینال اولیه
• I1 = جریان اولیه
• I2 = جریان ثانویه
• Ie = جریان تحریک
• Im,Xm = جریان و راکتانس مغناطیس شوندگی
• Ic,Rc = جریان و مقاومت مربوط به تلفات هسته
• R1 = مقاومت سیم‌پیچ اولیه
• R2 = مقاومت سیم‌پیچ ثانویه
• X1 = راکتانس نشتی اولیه
• X2 = راکتانس نشتی ثانویه

شکل 4: نمودار فازوری مدار معادل ترانسفورماتور

مدار معادل ارجاع داده شده به سمت اولیه و ثانویه

در مدار معادل ترانسفورماتور شکل ۳، ترانسفورماتور ایده‌آل را می‌توان با ارجاع همه کمیت‌ها به اولیه یا ثانویه به ترتیب، به سمت راست یا چپ مدار معادل جابه‌جا کرد. شکل 5 این موضوع را نشان می‌دهد. معمولاً این جابه‌جایی را انجام می‌دهیم، زیرا تحلیل ترانس را آسان خواهد کرد.

شکل 5: (الف) مدار معادل ترانسفورماتور ارجاع داده شده به سمت اولیه (ب) مدار معادل ترانسفورماتور ارجاع داده شده به سمت ثانویه

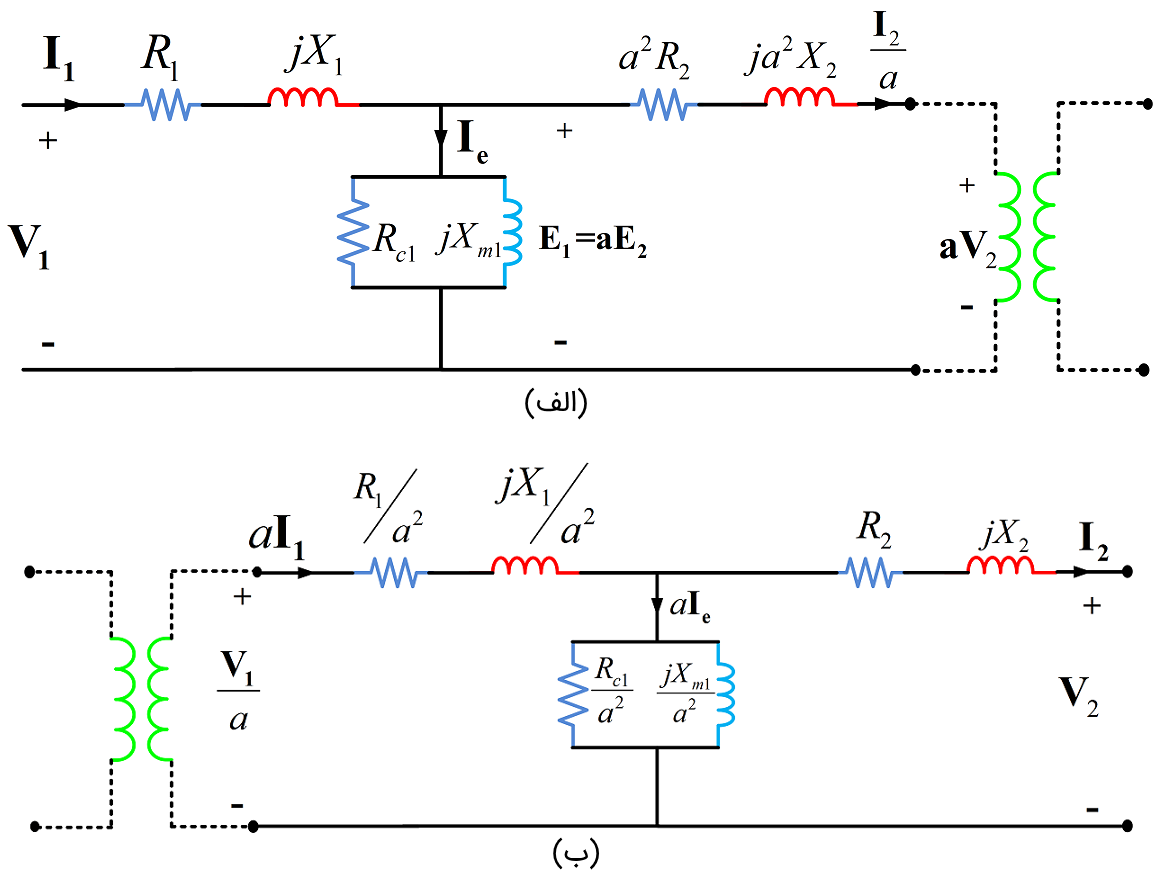
مدار معادل تقریبی ترانسفورماتور ارجاع داده شده به سمت اولیه و ثانویه

استخراج مدار معادل تقریبی از شکل 5 شروع می‌شود. همه کمیت‌ها به یک سمت ترانس ارجاع داده می‌شوند و می‌توان ترانسفورماتور ایده‌آل در مدار را حذف کرد.

1. اولین گام در فرایند ساده‌سازی، جابه‌جایی شاخه مغناطیس‌شوندگی شنت از وسط مدار T به ترمینال اولیه یا ثانویه است. شکل 6 (الف) و (ب)، این موضوع را نشان می‌دهد. در این مرحله، از افت ولتاژ سیم‌پیچ‌های اولیه و ثانویه ناشی از جریان تحریک، چشم‌پوشی می‌شود. البته، افت ولتاژ ناشی از بار را در نظر می‌گیریم.

 

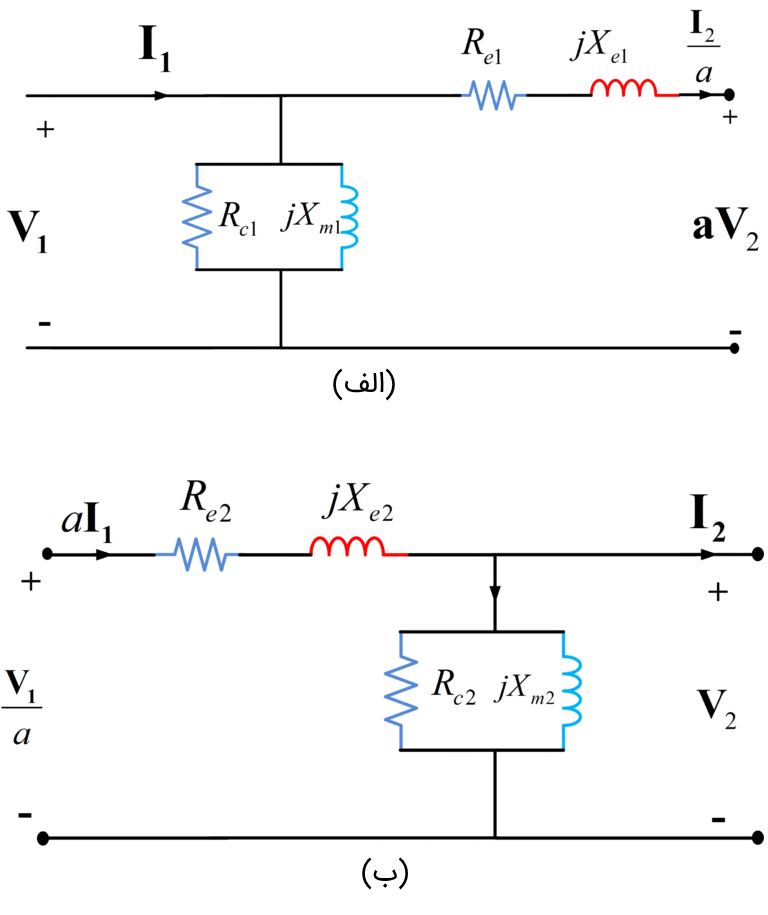
شکل 6: مدار معادل تقریبی شکل 5 (الف) و (ب)

2. مقاومت‌های سیم‌پیچ اولیه و ثانویه، برای مقاومت ارجاع داده شده به اولیه (Re1=R1+a2R2) در نظر گرفته می‌شوند. مقاومت معادل ارجاع داده شده به ثانویه نیز برابر Re20R1/a2+R2 است.

3. به طریق مشابه، راکتانس‌های سیم‌پیچ اولیه و ثانویه را می‌توان با هم ترکیب کرد و راکتانس معادل ارجاع داده شده به سمت اولیه را نوشت: Xe1=X1+a2X2. راکتانس ارجاع داده شده به ثانویه نیز برابر با Xe2=X1/a2+X2 است.

4. مرحله بعدی استخراج مدار معادل تقریبی، حذف کامل شاخه مغناطیس‌شوندگی موازی است. بنابراین، مدار معادل، به یک مدار ساده از امپدانس‌های سری تبدیل می‌شود که به اولیه یا ثانویه ارجاع داده شده‌اند. شکل ۷ (الف) و (ب)، مدار معادل تقریبی را نشان می‌دهد.

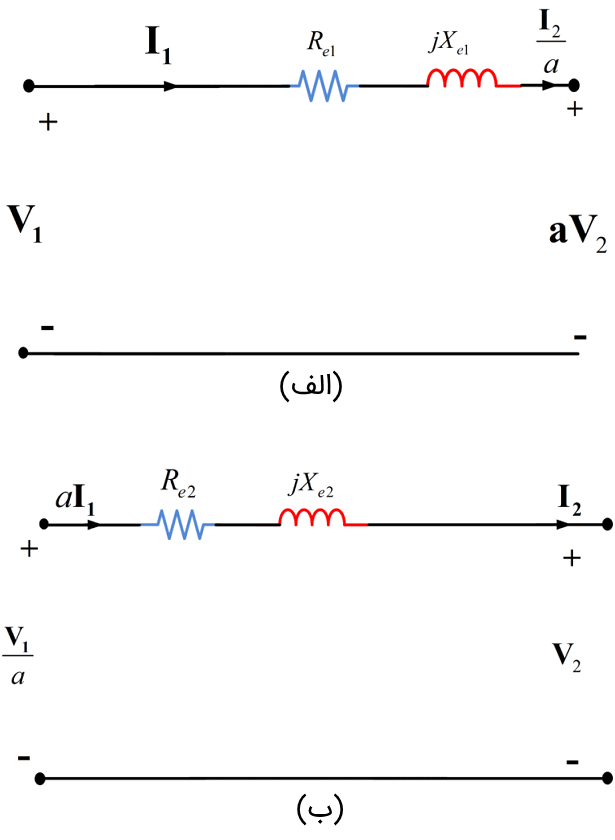
شکل ۷: مدار معادل تقریبی شکل 6 (الف) و (ب)